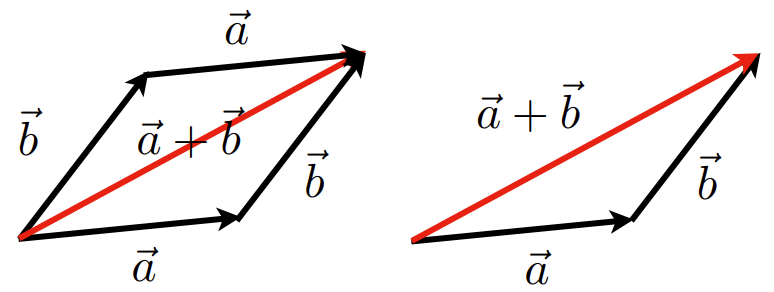Games101 Lecture 01 是一些图形学的基本介绍,我就不记录了,从 Lecture 02 开始
重点归纳:
- 向量点乘可以用于计算向量间的余弦夹角,从而得知向量互相的接近程度
- 向量点乘可以用于计算向量的投影,可以用于向量的分解,将向量分解成两个垂直的向量
- 向量点乘可以用于计算向量的方向性,判断两个向量是同向还是异向,以及它们的接近程度
- 向量叉乘的结果是一个向量,由右手螺旋定则决定方向
- 向量叉乘可以用于判断向量的左右关系,判断点在三角形的内部还是外部
- 矩阵在图形学中的应用:变换
阅读材料:Fundamentals of Computer Graphics(3rd or 4th), 第二章(Miscellaneous Math)、第五章(Linear Algebra)
A Swift and Brutal Introduction to Linear Algebra!
一、向量 (Vectors)
1. 向量的构成与特点
largea=AB=B−A
- 向量通常写作largea或者largea
- A 指向 B 的向量 = B 的坐标减去 A 的坐标
- 向量具有长度和方向两个属性
- 向量只要长度和方向相同就是相等的,并不关心其起始位置
2. 向量标准化 (Vector Normalization)
largea^=a/∥a∥
- 向量的长度被写作large∥a∥
- 单位向量 (Unit Vector) 就是长度为 1 的向量
- 单位向量用于表示方向而不关心其长度
3. 向量求和 (Vextor Addition)
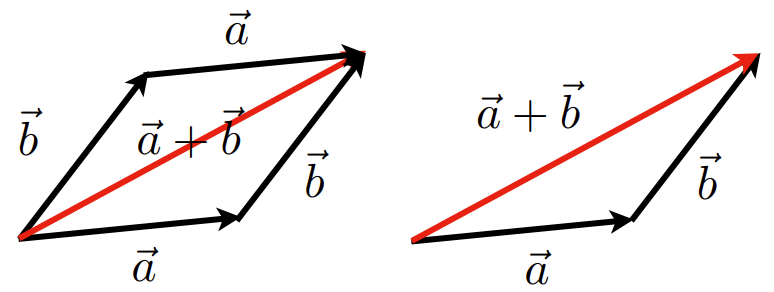
4. 向量的坐标表示 (Cartesian Coordinates)
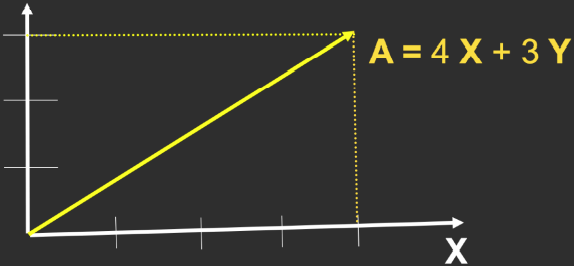
- largeX、largeY是正交(垂直在高维空间中的推广)的单位向量,分别是笛卡尔坐标系横轴和纵轴的方向
- 图形学上默认向量是列向量的形式:largemathbfA=left(beginarraylxyendarrayright)=left(beginarrayl43endarrayright)
5. 向量的点乘 (Vector Dot Product)
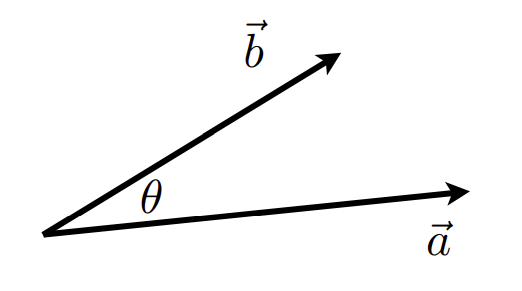
largea⋅b=∥a∥∥b∥cosθ
largecosθ=∥a∥∥b∥a⋅b
largecosθ=a^⋅b^
- 向量的点乘结果是一个值
- 已知两个向量的坐标表示,可以求他们之间的夹角,余弦夹角
- 两个单位向量的夹角就是他们的点乘
5.1 向量点乘的性质
largea⋅b=b⋅a
largea⋅(b+c)=a⋅b+a⋅c
large(ka)⋅b=a⋅(kb)=k(a⋅b)
- 当三个向量进行点乘时,后两个向量是不满足交换率和结合率的
5.2 在笛卡尔坐标系下的点乘计算
largevecacdotvecb=left(beginarraylxayaendarrayright)cdotleft(beginarraylxbybendarrayright)=xaxb+yayb
largevecacdotvecb=left(beginarraylxayazaendarrayright)cdotleft(beginarraylxbybzbendarrayright)=xaxb+yayb+zazbHuge
5.3 利用点乘求解投影 (Dot Product for Projection)
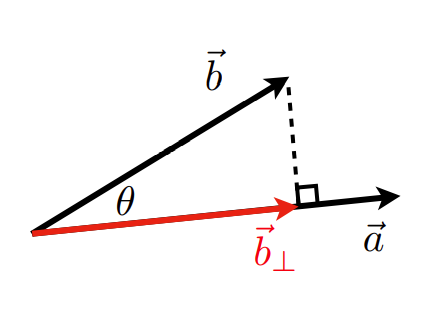
b⊥=ka^
k=b⊥=∥b∥cosθ
b⊥=∥b∥cosθa^=∥b∥a^b^a^=ba^a^
- 向量的投影可以用于分解向量,将b分解成两个互相垂直的向量 b_⊥ 和 b−b_⊥
5.4 利用点乘判断向量间的方向 (Dot Product in Graphics)
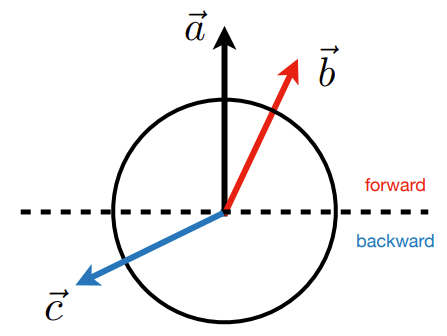
- 求解a和c、b的余弦夹角
- 若cosθ>0,则与a同向
- 若cosθ=0,则与a垂直
- 若cosθ<0,则与a异向
- 若cosθ越接近1,则越接近a
应用:金属的高光,镜面反射,用于判断出射光和相机法向的接近关系
6. 向量的叉乘 (Cross Product)
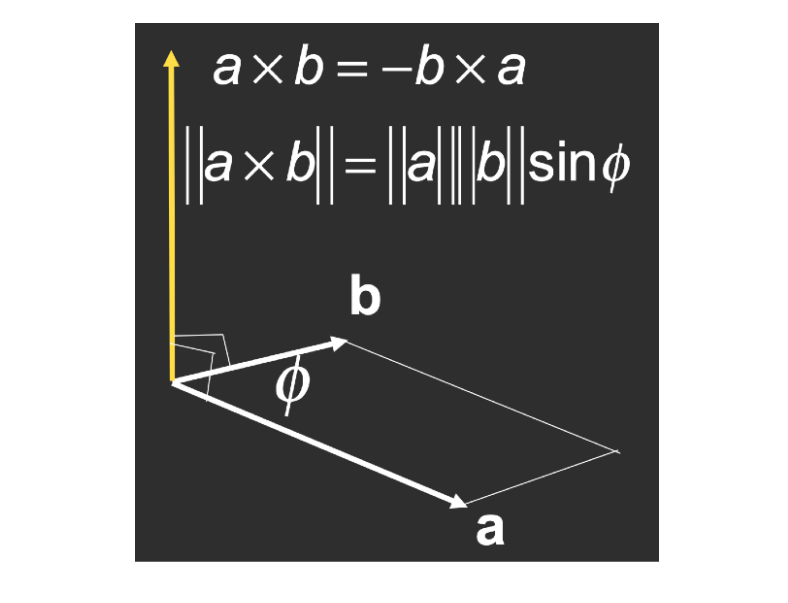
叉乘的结果是一个向量
- 右手螺旋定则确定叉乘的方向
- 向量的大小为 ∣a∣∗∣b∣∗sinθ
应用:
- 构造坐标系
- 判断坐标系的左右手:x×y 得到 z, 则说明坐标系的方向是右手坐标系,得到 −z则是左手坐标系
a×b=yazb−ybza zaxb−xazb xayb−yaxb
a×b=A∗b=0 za −ya−za0xaya−xa0xb yb zb
6.2 向量叉乘的性质 (Cross product: Properties)
x×y=+z y×x=−z y×z=+x z×y=−x z×x=+y x×z=−ya×b=−b×aa×a=0a×(b+c)=a×b+a×ca×(kb)=k(a×b)
6.3 向量叉乘的应用
判断向量的左右关系:

- 如图,a×b, 其 z 坐标大于 0, a在 b的右侧
- 如图,a×b, 其 z 坐标小于 0, a在 b的左侧
判断点在三角形的内部还是外部:
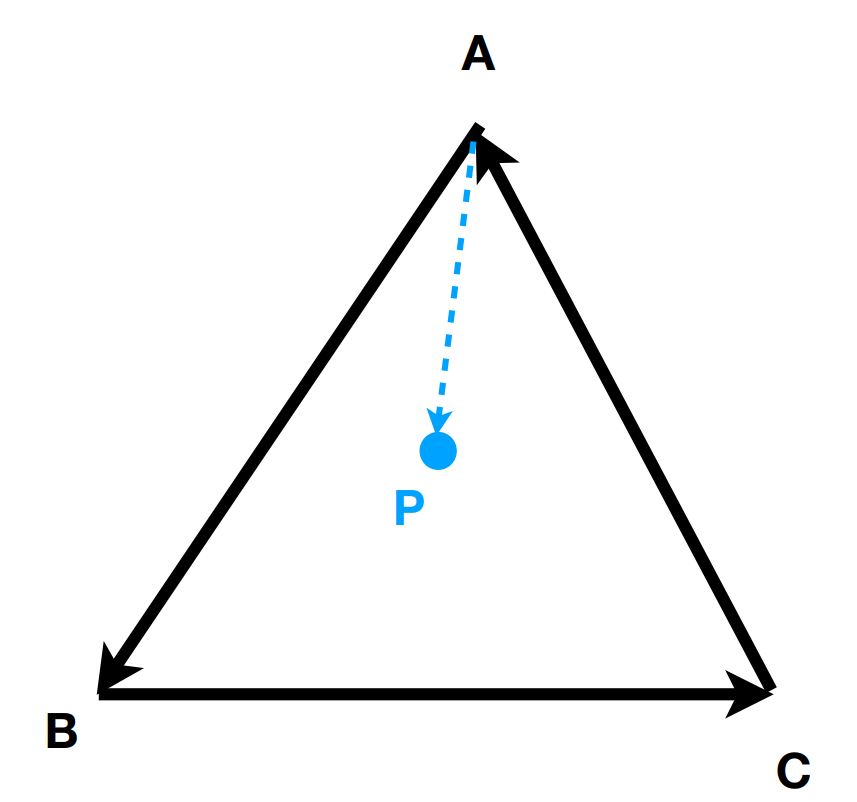
- AB×AP, 结果向外,P 在 AB 的左侧
- BC×BP, 结果向外,P 在 BC 的左侧
- CA×CP, 结果向外,P 在 CA 的左侧
- 则说明 P 在三角形 ABC 内部
对于三角形 CBA, 则 P 一定都在其右侧,如果刚好 P 点在与某一个向量的叉乘为 0, 与其他两个向量的叉乘为同侧,则说明 P 在三角形上,这种情况自己定义是在内部还是在外部
二、正交基与坐标系 (Orthonormal bases and coordinate frames)
1. 自定义坐标系
n∥u∥=∥v∥=∥w∥=1 u⋅v=v⋅w=u⋅w=0 w=u×v (right-handed)
- u^, v^, w^ 为互相垂直的单位向量
p=(p⋅u)u+(p⋅v)v+(p⋅w)w (projection)
- 向量p通过投影分解
三、矩阵 (Matrices)
主要应用于矩阵变换 (Transformations)
- Translation, Rotation, Shear, Scale
1. 矩阵乘法 (Matrix-Matrix Multiplication)
1 5 0324(3 2679843)
- 需要满足要求:(M x N) (N x P) = (M x P)
1 5 0324(3 2679843)=9 19 8?44283361321326?
- Element (i, j) in the product is the dot product of row i from A and column j from B
2. 矩阵乘法的运算律/性质(Properties)
(AB)C=A(BC)
A(B+C)=AB+AC
(A+B)C=AC+BC
3. 矩阵与列向量
- 在图形学中,向量用列向量表示是为了方便左乘一个矩阵
- 向量的点乘和叉乘都可以写成矩阵乘法
4. 矩阵的转置
135246T=(123456)
(AB)T=BTAT
5. 单位矩阵与矩阵的逆
I3×3=100010001AA−1=A−1A=I(AB)−1=B−1A−1