重点归纳:
- 2D 变换:
- 线性变换 (Linear):缩放 (scale)、切变 (shear)、旋转 (rotatrion)、镜像 (Reflection)
- 非线性变换:平移 (translation)
- 仿射变换 (Affine): 线性变换 + 平移
- 齐次坐标
- 变换的组合与分解
变换的分类:
- 模型变换 (Modeling):
- 观测变换 (Viewing):
- View(视图)/Camera 变换
- 3D 到 2D 的投影变换 (Orthographic/Perspective, 正交/透视)
1. 缩放 (scale)
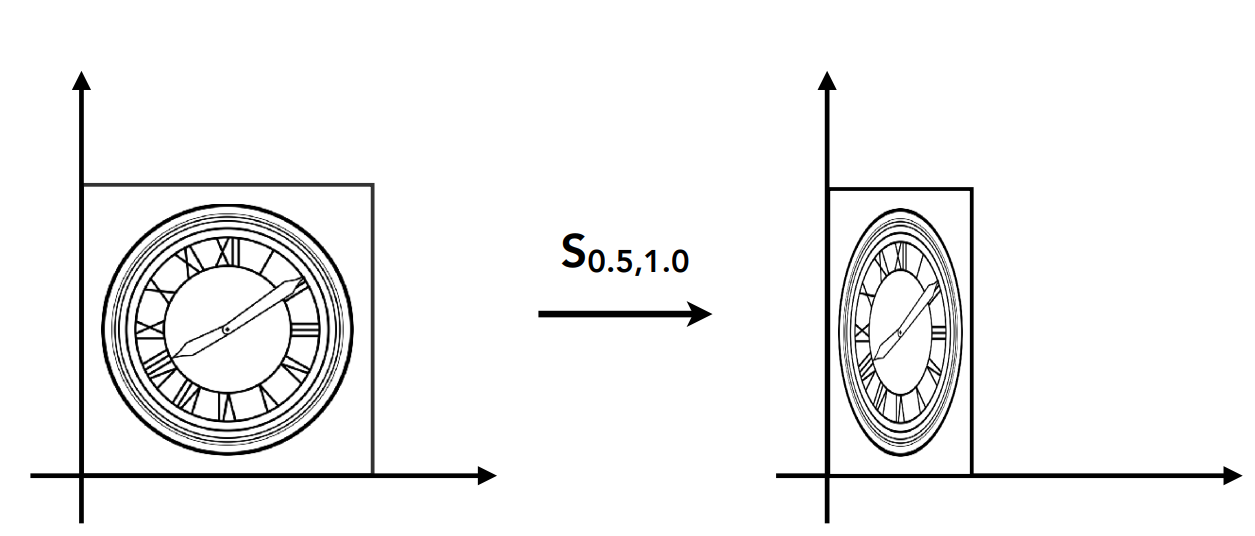
[x′y′]=[0.5001][xy]
2. 镜像 (Reflection)
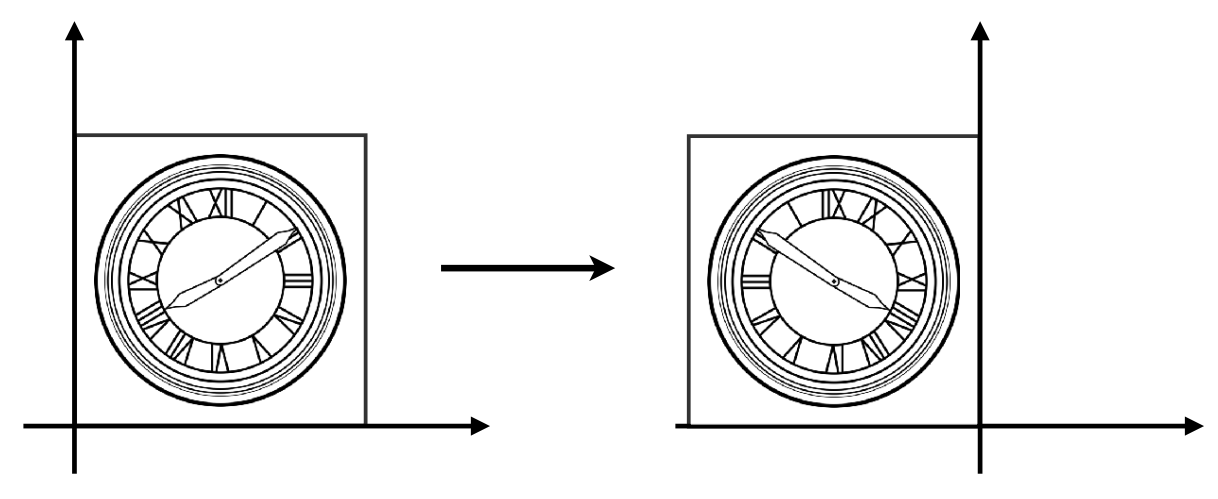
[x′y′]=[−1001][xy]
3. 切变 (shear)
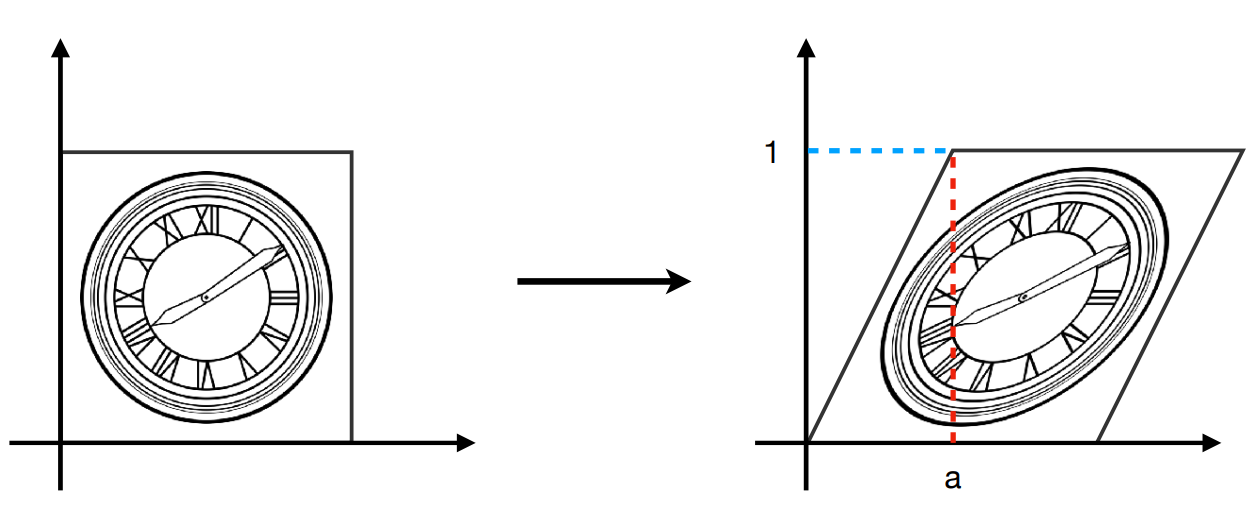
[x′y′]=[10a1][xy]
x′=x+ayy′=y
4. 旋转 (rotate)
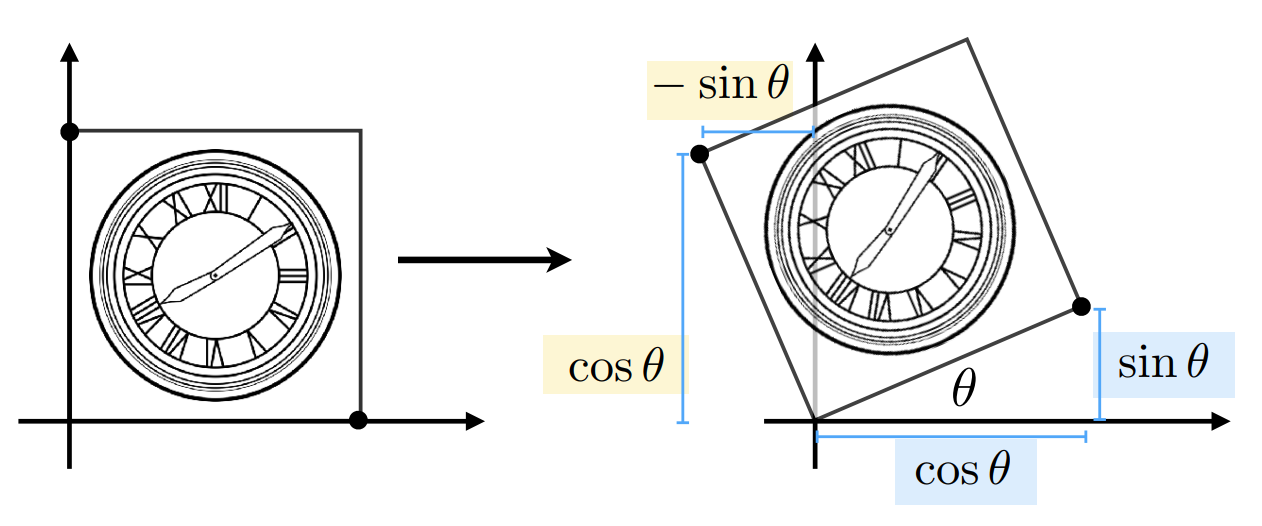
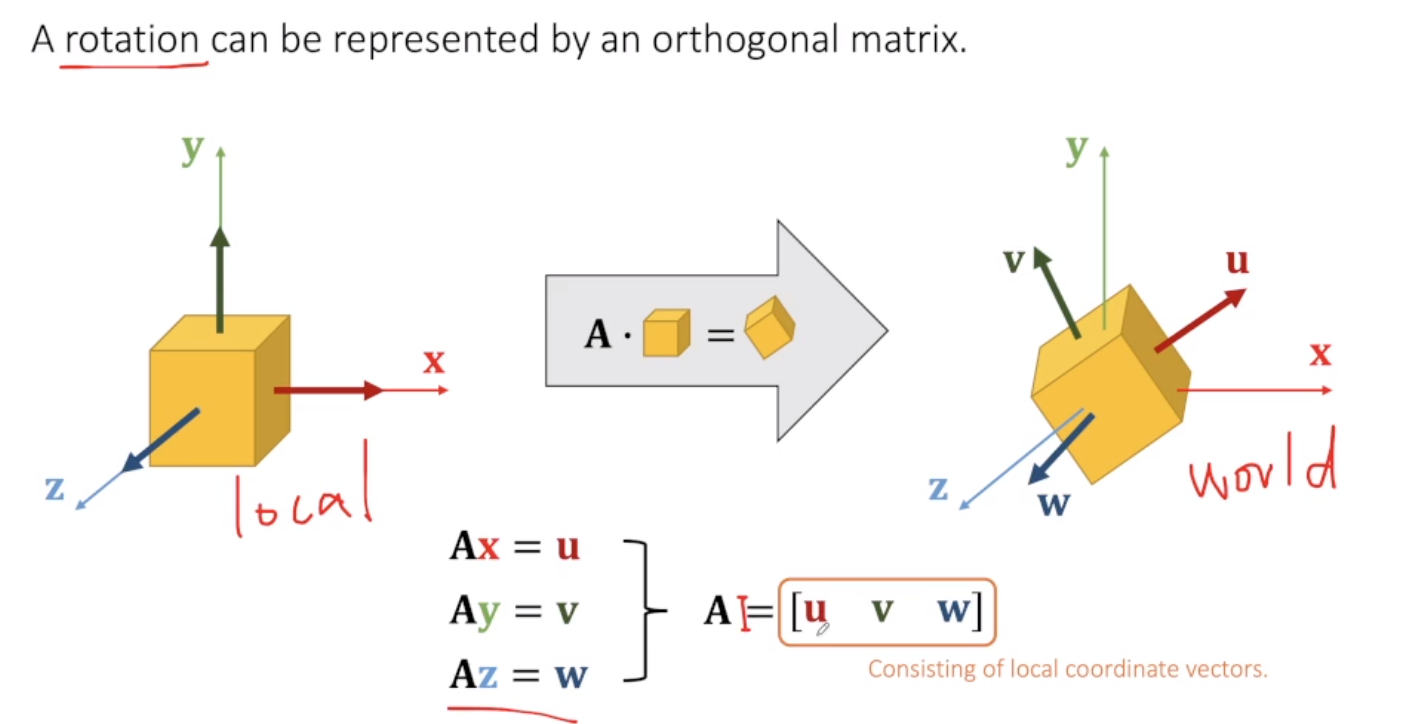
Rθ=[cosθsinθ−sinθcosθ]
同时旋转矩阵也是一个正交矩阵,因为其逆变换为旋转−θ, 也就是说其逆变换矩阵为:
R−θ=[cosθ−sinθsinθcosθ]
而该矩阵刚好是 Rθ 的转置
逆变换矩阵 = 变换矩阵的逆
正交矩阵即左乘其转置等于单位矩阵的矩阵
正交矩阵的逆等于其转置
正交矩阵的列向量为两两垂直的单位向量
关于旋转矩阵是正交矩阵,Games103 中也有一种解释,即旋转操作相当于对坐标系的旋转
线性变换的矩阵形式
x′=ax+byy′=cx+dy
[x′y′]=[acbd][xy]
x′=Mx
5. 平移 (translation)
x′=x+txy′=y+ty
平移变换虽然形式简单,但无法写成矩阵的线性变换
[x′y′]=[acbd][xy]+[txty]
二、齐次坐标 (Homogenous Coordinates)
1. 使用齐次坐标的目的
为了将以上的变换的矩阵形式统一起来而发明
- 2D Point = (x,y,1)⊤
- 2D Vector = (x,y,0)⊤
trade off/no free lunch:
- 优点:统一了仿射变换的矩阵形式
- 缺点:需要多一维的空间
同时也保证了运算的合理性
- vector + vector = vector
- point - point = vector
- point + vector = point
- point + point = ??
xyw is the 2D point x/wy/w1,w=0
可以推得,两个点相加得到的是他们的中点
2. 齐次坐标下,仿射变换矩阵的特点
Scale
S(sx,sy)=sx000sy0001
Rotation
R(α)=cosαsinα0−sinαcosα0001
Translation
T(tx,ty)=100010txty1
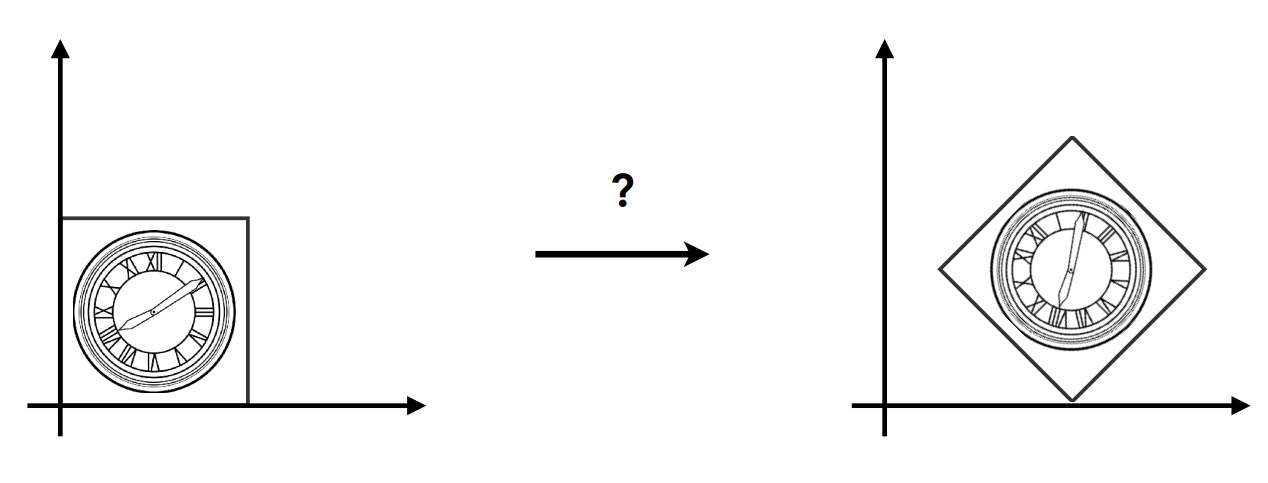
复杂变换可以通过简单变换得到
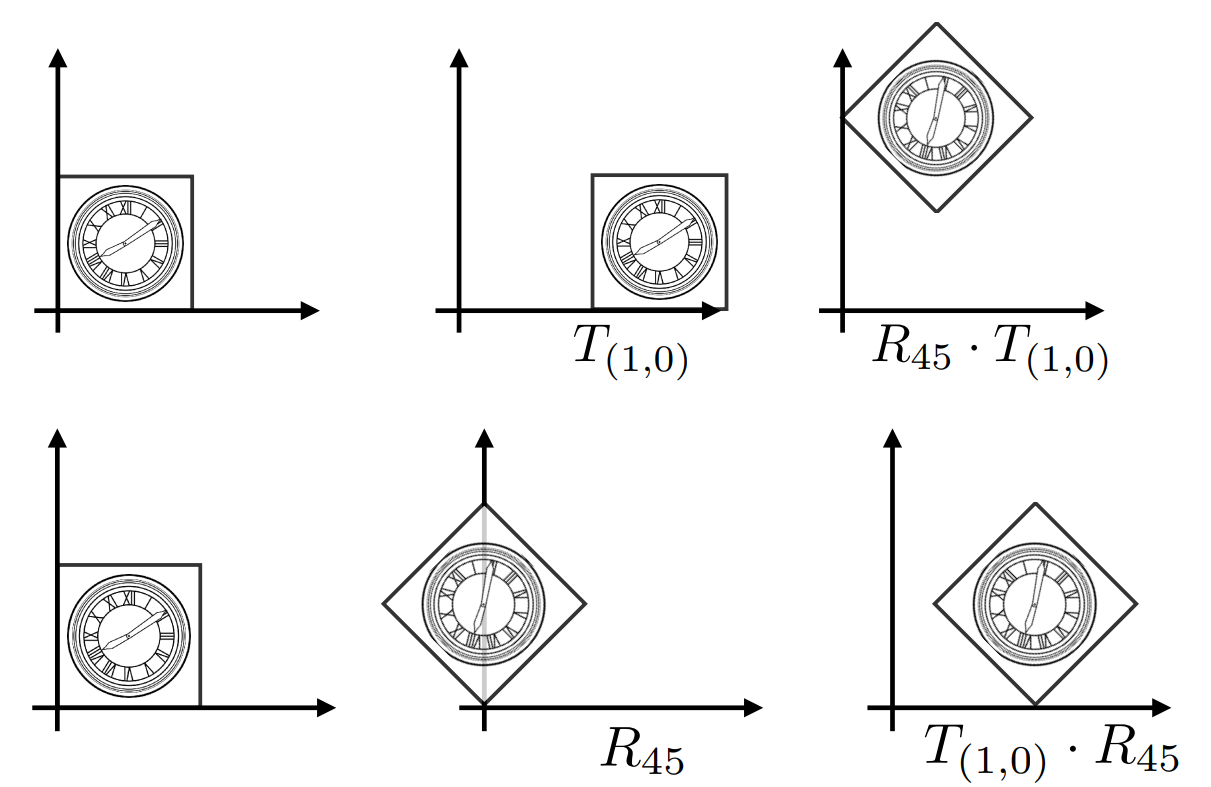
顺序很重要,先旋转再平移
T(1,0)⋅R45xy1=100010101cos45∘sin45∘0−sin45∘cos45∘0001xy1
矩阵乘法满足结合律,变换的顺序是从右到左,但计算的顺序可以从左到右
Q: 以任意点为中心旋转?
A: 变换的分解, 先平移到中心, 再旋转, 再平移回去
T(c)⋅R(α)⋅T(−c)
- 3D Point = (x,y,z,1)⊤
- 3D Vector = (x,y,z,0)⊤
对于第四维为 w 的点:
(x,y,z,w)=(x/w,y/w,z/w,1)
x′y′z′1=adg0beh0cfi0txtytz1⋅xyz1
Q: 齐次坐标下 4x4 的仿射变换矩阵是先线性变换?还是先平移 A: 相当于普通坐标下先线性变换再平移






